CAD 嵌入式 CFD 的数值基础(三)
连载中.上承CAD嵌入式CFD的数值基础(二),阅读全文请跳转至CAD嵌入式CFD的数值基础(二)
3)实体曲面之间和透明实体中的辐射
辐射是一个复杂现象,因此有很多简化的辐射模型。所有这些模型都有优点、缺点和限制。SOLIDWORKS Flow Simulation包括2个模型:
1.射线跟踪,也称作DTRM(离散传输辐射模型)。
2.离散坐标(DO)。
对于射线跟踪模型,来自实体曲面的热辐射,包括发射和反射,均假设为散射(对称和镜面辐射曲面类型除外),即:它们遵守朗伯定律。据此,每单位面积和每单位立体角的辐射强度在所有方向上均相同。曲面可吸收和反射太阳辐射,与热辐射无关。热辐射通过被指定为辐射透明的实体,不存在任何吸收。一个实体可被指定为仅对太阳辐射透明、或对太阳辐射以外所有热源的热辐射透明、或对热辐射和太阳辐射两种类型的辐射透明。此方案还可考虑折射。流体既不发射也不吸收热辐射(即:它们对热辐射是透明的),因此热辐射仅影响实体表面。未指定为黑体或白体的辐射实体曲面被假设为一个理想的灰体,即,具有与黑体相似的持续发射功率谱,因此其单色发射率与发射波长无关。对于具有特定曲面条件的特定材料,灰体发射率可取决于曲面温度。在射线跟踪模型中不考虑光谱依赖性。离散坐标模型更加复杂。在这里,计算域内任何位置处的整个4π 方向域被离散到特定数量的相等立体角中。辐射管理方程如下:
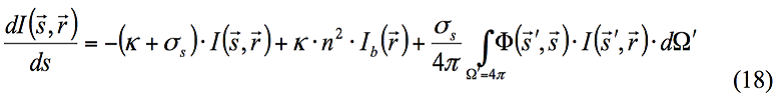
辐射吸收(半透明)实体依据规定的实体材料的吸收系数吸收并发射热辐射。未考虑散射。不透明实体曲面依据规定的辐射系数吸收热辐射,其余入射辐射依据规定的镜面反射系数被镜面反射、漫射或同时被镜面反射和漫射。依据实体和相邻介质的规定的折射指数进行折射(对于其他辐射吸收实体或透明实体或流体,折射指数始终应等于1)。辐射光谱被认为包含几个谱带,其边缘由用户指定。在各谱带中,辐射源、曲面和材料的属性被认为是常数。
由于辐射计算,在浸润流体-液体边界的部分单元中或在半透明实体内的实体单元中考虑适当的热通量。
4.边界层处理
非贴体笛卡尔网格适合于管理原始CAD数据,因而构成CAD/CFD桥接的基础。笛卡尔浸润体网格的主要问题在于对粗糙网格上的边界层进行求解。为此,SOLIDWORKS Flow Simulation技术包含了以下所述的原始方法,并且该方法与SOLIDWORKS Flow Simulation笛卡尔网格技术的组合构成了SOLIDWORKS Flow Simulation CAD/CFD桥接的主要部分。
对近壁单元的考虑表明,对于任意的原始CAD几何体,实体/流体边界之间的网格对于高梯度边界层内的纳维-斯托克斯方程的精确求解过于粗糙。因此,为计算壁的表面摩擦和热通量,采用了针对边界层的普朗特方法。该方法的核心思想与传统上CFD使用的壁函数方法有一些相似。作为构成SOLIDWORKS Flow Simulation平台技术的一部分,壁处理采用新颖而原始的两尺度壁函数(2SWF)方法,该方法包含2种方法,用于将边界层计算与整体流的求解相结合:
1.当越过边界层的单元数量不足以直接或简化确定流动和热曲线时使用“薄”边界层处理;
2.当越过边界层的单元数量超出精确求解边界层的数量时使用“厚”边界层处理。
3.在介于两者之间的情形时,综合采用了以上两种方法,以确保在细化网格时或边界层沿曲面增厚时两个模型之间能够平滑过渡。
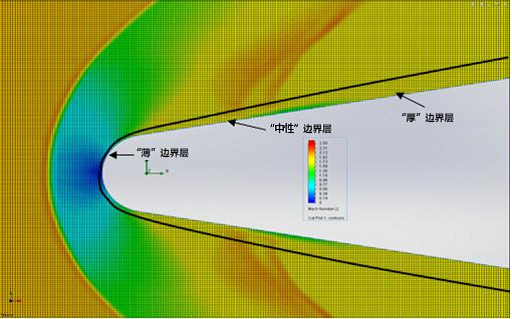
图12:具有“薄”、“中性”和“厚”粘性边界层的马赫数流场。
对SOLIDWORKS Flow Simulation技术边界层处理的验证由Balakine等(2004)完成。这些处理将在下文讨论。
1).薄边界层方法
在薄边界层方法中,已沿壁的法线方向(即沿体曲面坐标的法线方向)从0(在壁处)到边界层厚度 δ 集成的普朗特边界层方程已沿覆盖壁的流体流线进行求解。如果边界层为层流,这些方程式均采用基于Shvetz试探函数技术的逐次逼近求解方法(Ginzburg,1970)。如果边界层为湍流或过渡流,一般使用有关湍流边界层中混合长度的Van Driest假说的方法(VanDriest,1956)。
通过校正从流体到壁的壁剪切应力和热通量的半经验系数,对粗糙度影响(被视为相当沙粒粗糙度)和边界层上的外部流动湍流进行建模。在相应的经验和半经验模型中还应考虑流体压缩性、湍流动能耗散和各种体力。
从边界层计算中,SOLIDWORKS Flow Simulation得出边界层厚度 δ、壁剪切应力 τew和从流体到壁的热通qew,这些被用作纳维-斯托克斯方程的边界条件:

k和 ε 的边界条件通过近壁计算网格单元中的湍流平衡条件确定:

2).厚边界层方法
当越过边界层的单元数量充足时(大于~10),通过纳维-斯托克斯方程完成层流边界层的仿真,作为中心流计算的一部分。对于湍流边界层,采用了一种众所周知的壁函数方法的修正。然而,不同于采用对数速度曲线的经典方法,SOLIDWORKS Flow Simulation技术采用由VanDriest (1956)提出的全曲线:
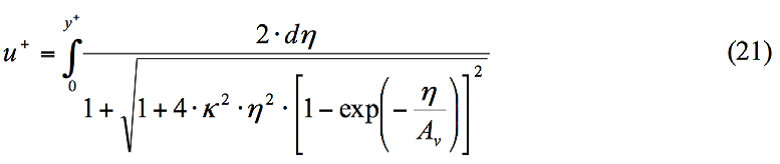
式中:к= 0.4054是Karman常数,Av = 26是Van Driest系数。
所有其他假设与经典壁函数方法类似。




